[WebMaster]

---

Algorithm

---

Pricing theories and complex market models offer some explanation as to how world equity markets operate. Concepts such as closed markets, arbitrage pricing, and single-index models are possible but require a central authority to function. An example of a closed market is the bulk purchase of lumber. Wood can no longer be bought directly from a sawmill; it must now be done through a broker. Although this regulation may seem unfair to some, it does serve a purpose: keep the price of lumber equal to the price of the commodity contract. A system that is harder to manage can be enforced with strict guidelines. The application of blockchain makes these exact pricing and system models easier to implement. The guidelines are built into the code and the operation of the blockchain. This closed market concept is good because the sawmills can maintain the price set by the commodity market, ensuring fair value for the effort. Price discovery for the sawmills was localized, and if a mill were having a hard time selling wood, they would have been able to sell cheaper, hurting their bottom line in the long run.

Price discovery has been the dominant market model that has evolved over several decades, particularly around computers. As nearly all trading (equities, commodities, currencies, etc.) activities are done on computers, different market valuations and high-frequency trading can take advantage of various arbitrage situations, even fostering price manipulations that have become harder to track. Stock exchanges such as Dow, S&P, etc., also pay large-volume traders to ensure that liquidity remains in the markets; essentially, they are paid to trade with themselves.

The above lumber example resembles the VTB model, mainly controlling the price. However, the VTB price is controlled using a blockchain. A specific algorithm sets the value, ensuring the price during the transaction stage. With any risk-free asset, the price is determined by time and users’ support, which keeps it liquid. These are the same characteristics seen in bond markets. Cryptocurrency exchanges behave similarly to the legacy lumber market, whereby the price of assets such as BTC or ETH fluctuates from one exchange to another. This fluctuation creates a pricing discrepancy that can potentially lead to problems, such as illiquidity, as seen during the localized flash crashes of BTC and ETH in the past couple of years.

The VTBC pricing method was conceived to prevent this potential predicament (local flash crashes) and others by having the price controlled by the blockchain. As a result of enforcing the algorithmic pricing of the digital VTBC asset, an equalized price is set for all users while removing the need for price discovery, arbitrage, and zero-sum complications. VTB has advantages for all, including traders, who can park assets in VTBC to wait for the next dip in integrated cryptocurrencies.

The value algorithm was built upon simple concepts: bank on a minimum increase following a 30-year curve and offer potential upside on top of the curve. Logically, increased usage of the asset produces a higher value. Since pricing is controlled, value fluctuations are drastically mitigated. The algorithm is also designed not to reduce the upside of the oscillations.

2021	2022	2023	2024	2025	2026	2027	2028	2029	2030
100%	90%	85%	82%	80%	78%	75%	72%	70%	68%
2031	2032	2033	2034	2035	2036	2037	2038	2039	2040
65%	62%	60%	58%	55%	50%	48%	45%	42%	40%
2041	2042	2043	2044	2045	2046	2047	2048	2049	2050
38%	35%	30%	28%	25%	24%	23%	22%	21%	20%

The increase is in two parts, per hour and the completion of a purchase. As seen above, part of the algorithm has an annual decreasing curve starting at 100% and ending at 20% (at the end of 30 years). The ending value of 20 percent will continue each year afterward. These values are subject to change. The algorithm calculates the expected price increase and selects the larger hourly raise price or the transactional raise. This ensures the annual increase is met hourly but leaves room for unlimited user-based growth.

The usage part of the increase considers several project-specific factors, including order book value and transaction value. The calculation is performed on a sliding scale of > 0 to 0.0005 per base value ($50 to start) and time-based fluctuations on the VTBC value. Akin to a seesaw mechanism, as the VTBC increases from $1 to $2, the base value decreases to $25. Likewise, as the order book sales value increases, the scale of > 0 to 0.0005 decreases to maintain liquidity. The base value will continue to decrease as the price rises to maintain a consistent percentage increase over time compared to the current price, i.e., if the price is $4 or $400, the price increase per base amount in terms of percentage will remain the same.

Below, you can see the algorithm and its use of different variables.

Then, the equation for time can be written as follows:

Bringing the two together:

The increase according to equation 2 during the period between hour h and the next hour h+1:

Assuming that the price increases 3 times by transaction:

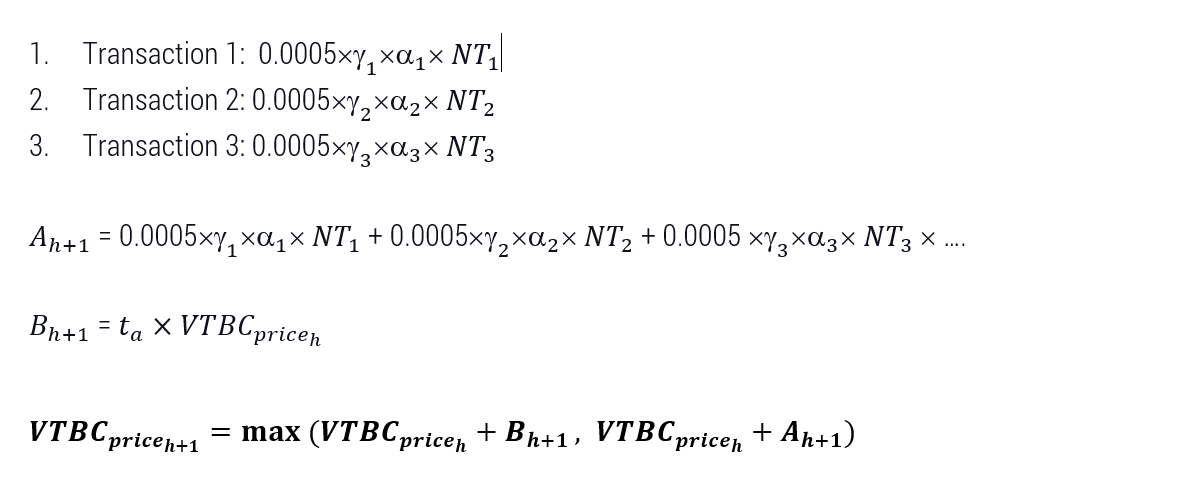
The equation for use increase is defined by the following:

M: is the price of a transaction at the beginning of the system and his value is $50.

NT: number of current transactions (C/M=1000/50=20 transactions)

We assume by:

Here are some examples of the formulas:

Here is an example of the use and time-based formulas combined:

Therefore, the return generated by a VTBC holder over 30 years will be unprecedented; however, given the current cryptocurrency climate, similar or even higher results could be achieved through day-trading or other investment instruments.

This project should be perceived as a steady and predictable method to achieve expected value increases.

You may consult our White Paper for a complete reference of this whole section at https://bit.ly/vtbwhitepaper

[Author]

Posts